A. INTRODUCTION
B. GRAPH THEORY
C. GLOSSARY OF TERMS USED FOR NETWORK ANALYSIS
D. ILLUSTRATIONS OF SOME KEY TERMS IN THE GLOSSARY
A. INTRODUCTION
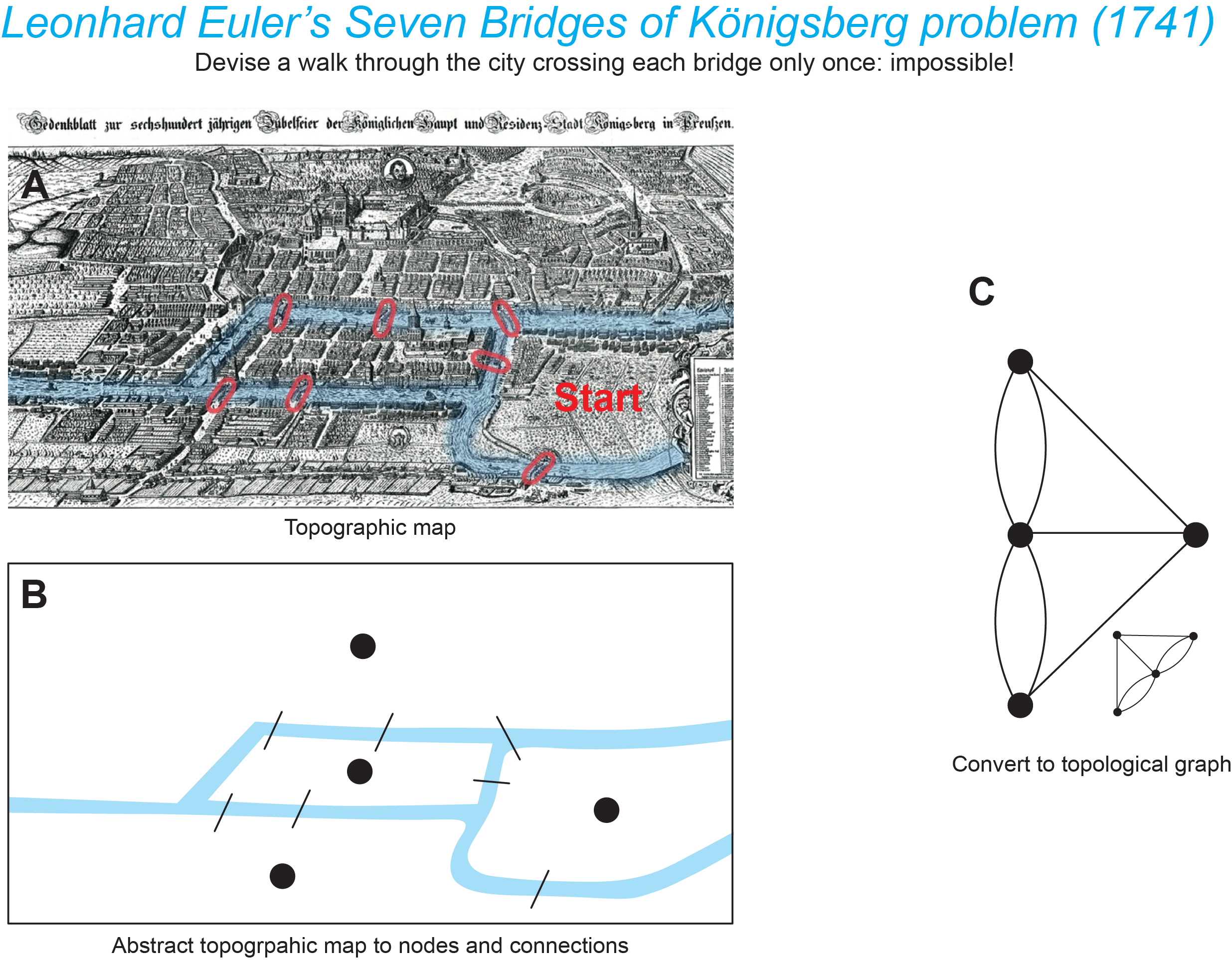
Network science can be viewed as an interdisciplinary study of the structure and function of complex interconnected systems. Network neuroscience currently is based largely on graph theory, which was basically “invented” by Leonhard Euler, who presented his solution of the “Seven bridges of Königsberg problem” in 1736 at a lecture that was published in 1741. A map of Königsberg at that time (it’s now Kaliningrad, Russia) is shown in part A of the figure below. The problem in a nutshell was to devise a walk through the city that would cross each bridge once and only once. His rigorous analysis showed that this is impossible, and he did it by abstracting the problem as shown in part B: there are 4 land masses (which he represented as dots or nodes) and 7 bridges (connections or edges) between them. From these elements he then formed a graph (part C), which is topological rather than topographic–distance, orientation, and location are not considered, just relationships (for more on this topic see Seven Bridges of Königsberg).
B. GRAPH THEORY
Graph theory has been applied to large-scale nervous system networks only since around the turn of the 21st century, and so is still at relatively early stage of development. So far, its most widely-used applications are in human brain analyses based on structural and functional MRI, diffusion tensor imaging, magnetoencephalography, and electroencephalography (see Bullmore & Sporns 2009). However, attention is focused here on applications to neural networks and connectomes established with experimental pathway tracing methods in animals, where neuronal cell bodies with their dendrites, axons, and axon terminals can be resolved histologically.
C. GLOSSARY OF TERMS USED FOR NETWORK ANALYSIS. For a complementary list of defined terms used to describe anatomical (structural) connections click here.
D. ILLUSTRATIONS OF SOME KEY TERMS IN THE GLOSSARY
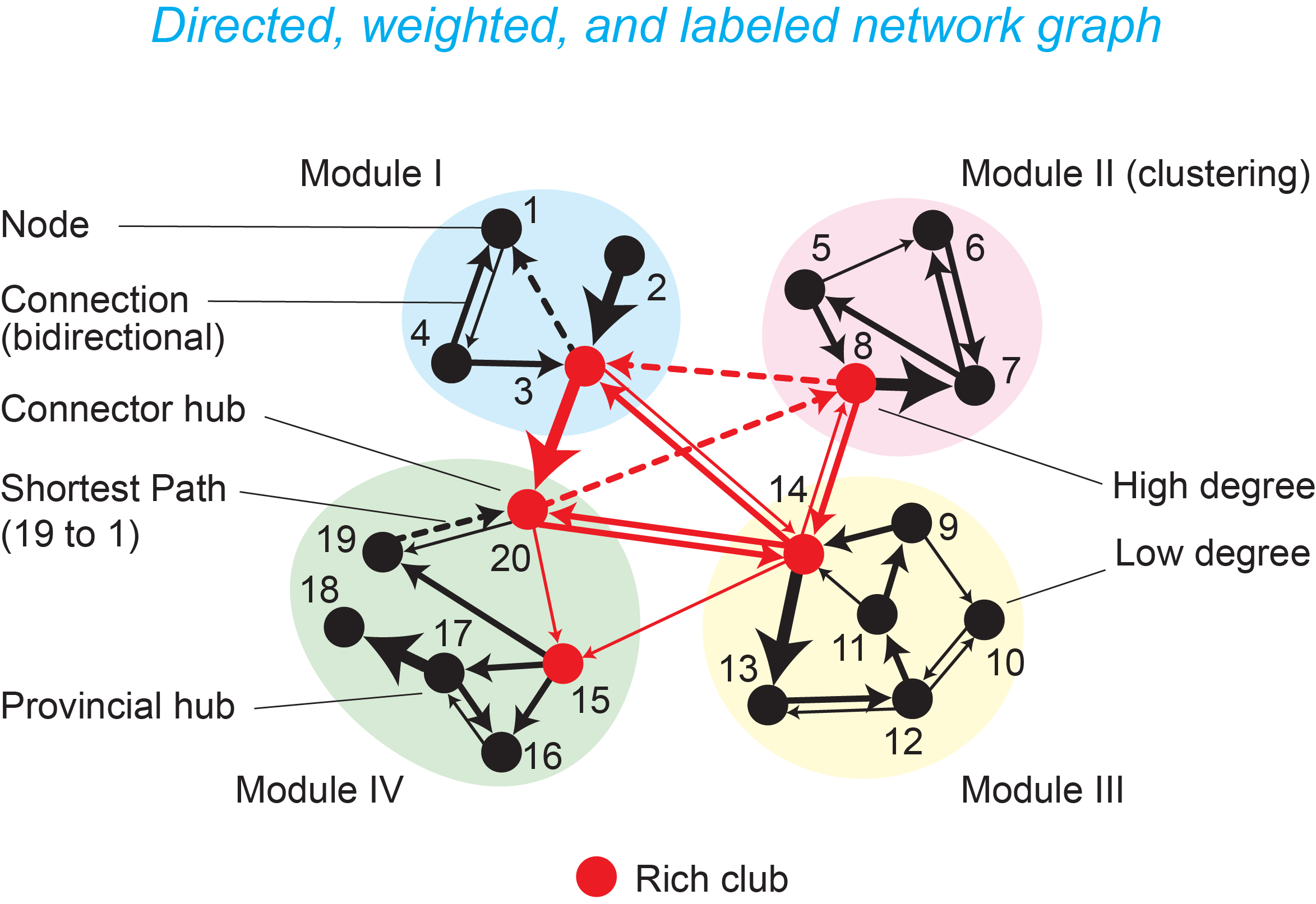Some basic features of a neural network graph (L.W. Swanson, unpublished, 2015).
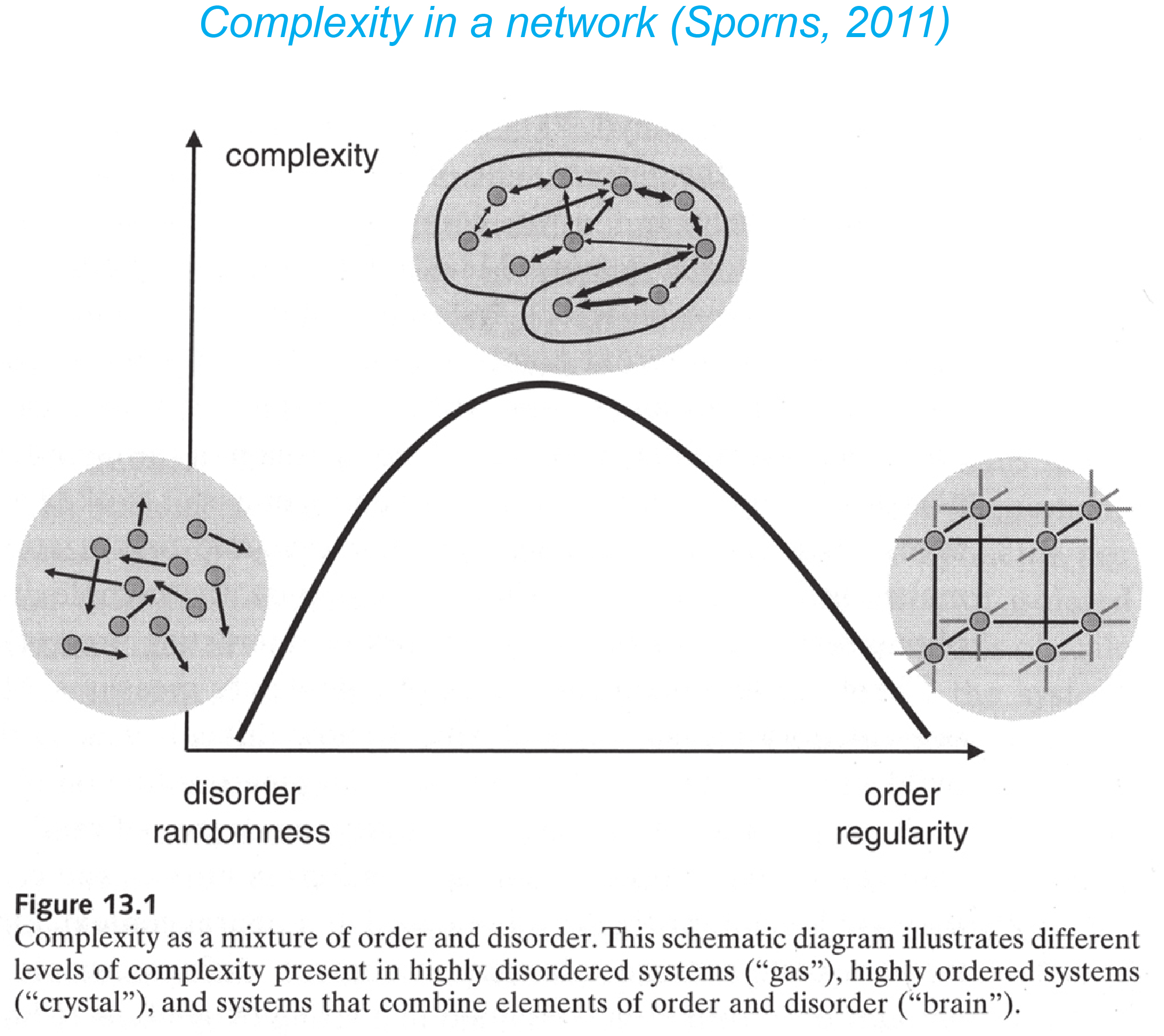
Possible modular organization of a graph (Sporns, 2011).
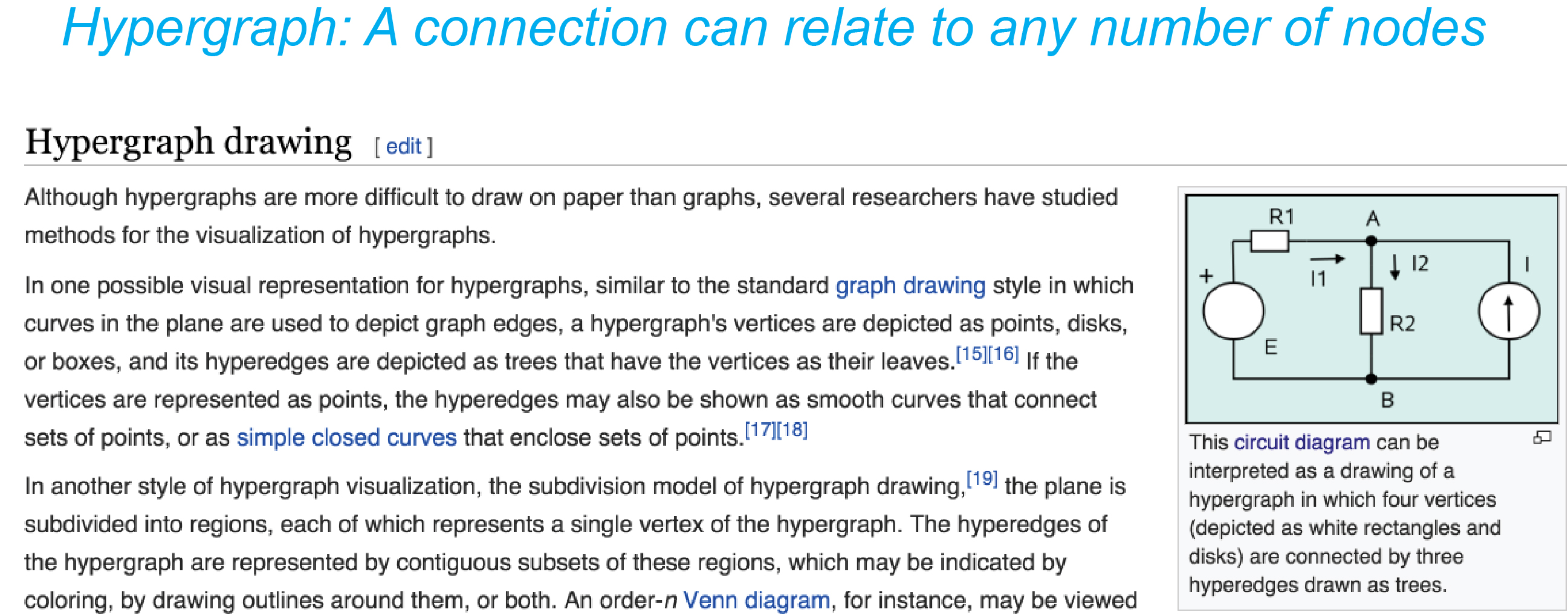Approach to microconnectome networks with axon branching (Wikipedia, Hypergraph).